Heapsort (Heapsort) fait référence à un algorithme de tri conçu à l'aide de la structure de données du tas. L'empilement est une structure qui se rapproche d'un arbre binaire complet et satisfait en même temps la propriété d'empilement : c'est-à-dire que la valeur de clé ou l'index d'un nœud enfant est toujours inférieur (ou supérieur) à son nœud parent. Le tri par tas peut être considéré comme un tri par sélection qui utilise le concept de tas pour trier. Il existe deux méthodes :

Grand tas supérieur : la valeur de chaque nœud est supérieure ou égale à la valeur de ses nœuds enfants, utilisée dans l'algorithme de tri de tas pour l'ordre croissant ;
petit tas supérieur : la valeur de chaque nœud est inférieure ou égale à la valeur de ses nœuds enfants, dans le tas L'algorithme de tri est utilisé pour trier par ordre décroissant.



Étapes de l'algorithme (en prenant la construction d'un grand tas supérieur comme exemple)

     Les étapes pour trier de petit à grand sont les suivantes :

1. Construire une séquence de longueur n en un grand tas supérieur ;
2.
Échanger le nœud racine avec le dernier nœud de la séquence, et le dernier nœud est la valeur maximale de la séquence ;
3. Convertir le nœud n - 1 restant est
4. Répétez les étapes 2 et 3 jusqu'à ce que la taille du tas
soit de 1 et qu'une séquence entièrement ordonnée soit construite.


     Le tas doit remplir deux conditions :
1. Il s'agit d'un arbre binaire complet (Complete Binary Tree)
2.
Chaque nœud du tas doit satisfaire que la valeur du nœud parent est supérieure ou égale à la valeur du nœud enfant ou la valeur du nœud parent est inférieure ou égale à La valeur du nœud enfant. parent >= enfants ou parent
<= enfants

Diagramme d'algorithme
      Nous prenons int
tree[] = {6, 10, 3, 8, 5, 12, 7, 2, 9} comme exemple pour illustrer le processus d'exécution du tri par tas.


Étape 1 : Construisez un grand tas supérieur à partir de la séquence d'origine (un grand tas supérieur est utilisé pour l'ordre croissant et un petit tas supérieur est utilisé pour l'ordre décroissant).
1. Construisez d'abord un arbre binaire complet à travers la séquence de haut en bas et de gauche à droite.

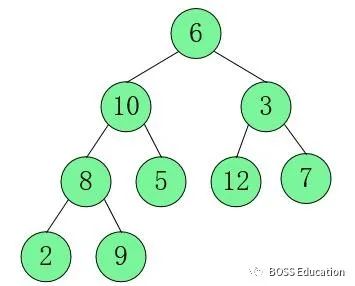
image

2. Ajustez le nœud parent de la troisième couche et le nœud enfant de la quatrième couche, où le rose représente le nœud qui échange. Faites en sorte que son nœud parent soit supérieur à deux nœuds enfants. C'est-à-dire en partant du dernier
nœud non-feuille (8 - 1) / 2 = 3, c'est-à-dire en partant de 8 et en ajustant de gauche à droite et de bas en haut.
Dans [8,2,9], 9 est le plus grand, échangez 8 et
9.

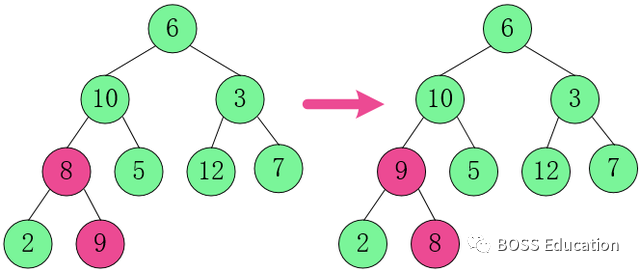
image

3. Ajustez le nœud parent du deuxième calque et le nœud enfant du troisième calque.
Dans [10,9,5], 10 est le plus grand, pas d'échange.
Dans [3,12,7], 12 est le
plus grand, échangez 3 et 12.

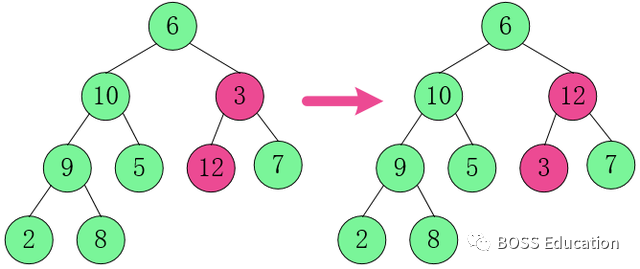
image

4. Ajustez le nœud parent du premier calque et le nœud enfant du deuxième calque.
Dans [6, 10, 12]
, 12 est le plus grand, échangez 6 et 12.

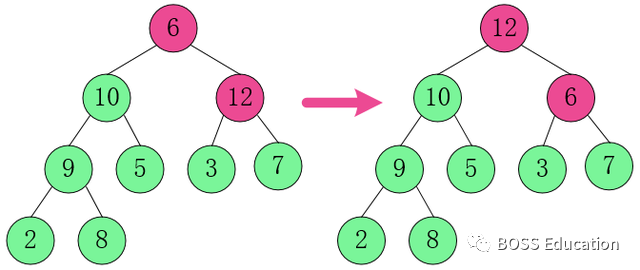
image

À ce moment, l'opération ci-dessus a pour résultat que [6,3,7] n'est pas un grand tas supérieur et continue de s'ajuster.
Dans [6,3,7], 7 est le plus grand, échangez 6
et 7.

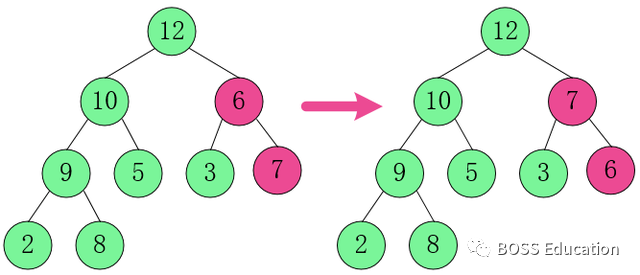
image

À ce stade, la construction du grand tas est terminée.

Étape 2 : Ajustez le nœud racine à la dernière position afin que le dernier élément soit le plus grand. Continuez ensuite à ajuster le tas pour les éléments restants, le nœud racine est ajusté à la dernière position et le deuxième plus grand élément est obtenu. Échangez, rechargez, échangez encore et encore.
1.
Échangez l'élément de nœud racine 12 avec 8.

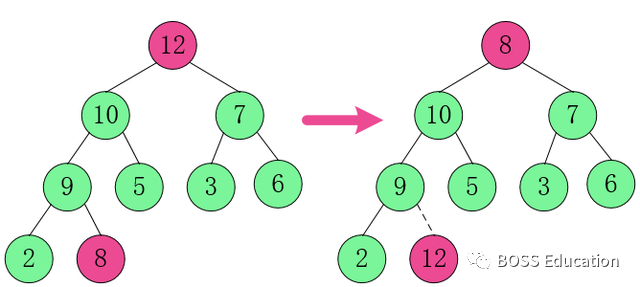
image

2. Restructurez la structure afin qu'elle continue à satisfaire la définition de tas.

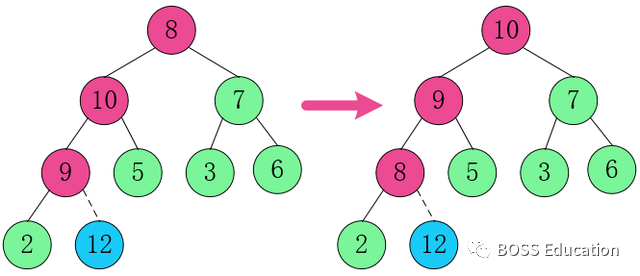
image

3. Échangez l'élément de nœud racine 10 avec 2.

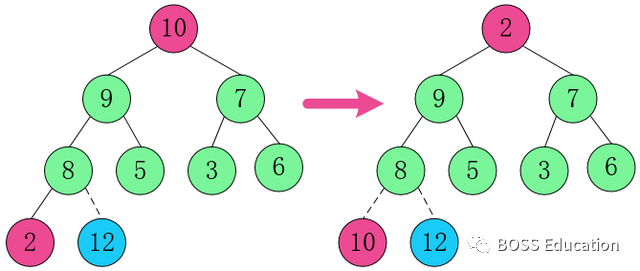
image

4. Restructurez la structure afin qu'elle continue à satisfaire la définition de tas.

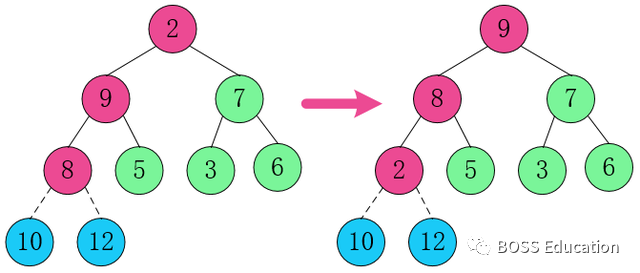
image

     Cela a été échangé, refactorisé, échangé...
Enfin, tous les éléments ont atteint un état ordonné.

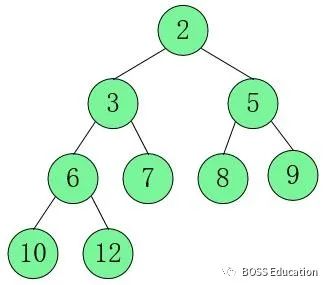
image



Solution en Python

import randomSampleList=random.sample(range(1,1000),9)print("乱序排列为：")print(SampleList)
def MaxHeapify(arr, dad, end):    maxkey=dad    lson = 2 * dad + 1  # left = 2*i + 1    rson = 2 * dad + 2  # right = 2*i + 2    if lson <= end and arr[dad] < arr[lson]:        maxkey = lson    if rson <= end and arr[maxkey] < arr[rson]:        maxkey = rson    if maxkey != dad:        arr[dad], arr[maxkey] = arr[maxkey], arr[dad]  # 交换        MaxHeapify(arr, maxkey, end)
def HeapSort(arr):               # 建大堆。    end = len(arr)-1    for i in range(end, -1, -1):        MaxHeapify(arr, i//2-1, end)        # 一个个交换元素    for i in range(end , 0, -1):        arr[i], arr[0] = arr[0], arr[i]  # 交换        MaxHeapify(arr, 0, i-1)
HeapSort(SampleList)n = len(SampleList)print("堆排序结果为：")print(SampleList)

Solution  en C++
#include<iostream>#include<cstdlib>#include<ctime>using namespace std;
void MaxHeapify(int arr[], int start, int end);void HeapSort(int arr[], int len) ;int print(int A[],int n); 
int main(){    int n=11;     srand((unsigned int)time(0));    int A[n];    for(int i=0;i<n;i++)    {        A[i]=rand()%1000;    }    cout<<"乱序排列为："<<endl;     print(A,n);    HeapSort(A, n) ;    cout<<"堆排序结果为："<<endl;     print(A,n);     return 0; }
int print(int A[],int n){    for(int i=0;i<n;i++)    {        cout<<A[i]<<"   ";    }    cout<<endl;    return 0;}
void MaxHeapify(int arr[], int dad, int end)//此函数是判断大小并执行交换 {      int maxkey = dad;//获取父节点的下标，暂时认为父节点数值最大    int lson = dad * 2 + 1;//左儿子节点，因为下标0开始所以需要+1    int rson = dad * 2 + 2;//右儿子节点，因为下标0开始所以需要+2
    if (lson <= end and arr[lson] >arr[dad]) //先比较左儿子节点和父节点，选择最大的         maxkey=lson;//若符合条件，指向左儿子节点     if (rson <= end and arr[rson] >arr[maxkey]) //比较右儿子(如果有)节点和max(左儿子节点,父节点)，选择最大的        maxkey=rson;//若符合条件，指向右儿子节点    if (maxkey!=dad)
    {    swap(arr[dad], arr[maxkey]);    MaxHeapify(arr, maxkey, end);  //儿子节点一旦与父节点交换值，儿子节点要继续与下级节点比较大小  }    } void HeapSort(int arr[], int len) {    //初始化，i从最后一个父节点开始调整，也就是从下到上进行调整，    for (int i = len / 2 - 1; i >= 0; i--)//15个元素，最后一个父节点下标是6        MaxHeapify(arr, i, len - 1);//数组下标是从0开始，所以end是len-1     //执行到这一步就已经符合大根堆的结构了     //使顶堆跟最后一个元素交换，这里i--达到弹出的效果，也就是i+1到len-1的范围都是已经排好序的，再重新调整使符合大根堆，直到排序完毕    for (int j = len - 1;j >= 0; j--)     {        swap(arr[0], arr[j]);        MaxHeapify(arr, 0, j - 1);    }}


















image


▍Avis de non  -responsabilité : Cet article est organisé à partir d'Internet. En cas d'infraction, veuillez contacter pour le supprimer.


Ce compte officiel publie cet article dans le but de transmettre plus d'informations. S'il y a une erreur dans l'étiquetage de la source ou une violation de vos droits légaux, n'hésitez pas à nous contacter pour consultation, contact (QQ): 993225721, nous le corrigerons et le supprimerons à temps.





Je vous aime pour nous suivre-